这是一个专门讨论 idea 的地方。
每个人的时间,资源是有限的,有的时候你或许能够想到很多 idea,但是由于现实的限制,却并不是所有的 idea 都能够成为现实。
那这个时候,不妨可以把那些 idea 分享出来,启发别人。
每个人的时间,资源是有限的,有的时候你或许能够想到很多 idea,但是由于现实的限制,却并不是所有的 idea 都能够成为现实。
那这个时候,不妨可以把那些 idea 分享出来,启发别人。
这是一个创建于 1850 天前的主题,其中的信息可能已经有所发展或是发生改变。
有这么一个函数 f(x, y),其中 x, y 都是非负整数,f(x,y) 的值为非负实数。
已知 f 满足如下条件:
- f(x, 0) = 0 对任何 x 成立
- f(0, y) = y 对任何 y 成立
- f(x, y) = f(y-1, y) 对任何 x >= y > 0 成立
- f(x, y) = [xf(x+1, y-1) + yf(x-1, y+1)] / (x+y) 对任何 y > x > 0 成立
请写出一个程序,可以计算 f(10000, 10000) 的值。
给出可行解的朋友可以留二维码地址,有红包打赏。
1
huabalance 2020-08-12 11:54:40 +08:00
`f(x, y) = [xf(x+1, y-1) + yf(x-1, y+1)] / (x+y) 对任何 y > x > 0 成立`
这一条会导致无尽的循环。例子:x=2, y=3 |
2
rekulas 2020-08-12 13:13:05 +08:00
@huabalance 2,3 还可以通过变形计算出来,但是还有很多这样的组合,可能不能通过常规递归方法来计算
|
3
mathzhaoliang OP @huabalance 你要是直接调用递归是不行的。实际上 f(2,3) 可以解方程组解出来。
|
4
huabalance 2020-08-12 17:07:47 +08:00
|
5
hebin 2020-08-12 22:58:02 +08:00 via iPhone
没有很懂 第三个不是可以推出来 f x y = f 0 y = y , 第四个又能随便算出如 f 1 2 != 2,
|
6
mathzhaoliang OP @hebin 第三个关系式到了 f(y-1, y) 以后,由于 y-1 < y 就不满足 3 了。
|
7
no1xsyzy 2020-08-13 15:05:57 +08:00
|
8
mathzhaoliang OP @no1xsyzy 虽然我没看懂,但是看到了求逆和计算矩阵乘法,感觉思路有点靠谱。但是对 n=10000 的情形运行太慢了。
|
9
mathzhaoliang OP @no1xsyzy 你的程序逻辑是对的,就是有点太慢了,对 x = y = 10000 的情形跑不动。
|
10
xml123 2020-08-13 22:44:32 +08:00
只能算个 x=y=1000 的规模
|
11
ITJoker 2020-08-14 23:47:01 +08:00
我有个思路,前面的老哥写的代码虽然遍历可能太慢。
但是如果我们另寻他路,我不知道可不可以, 首先先生成( 0,100 )的数字 求出 f(x,x)的值,例:f(1,1) , f(2,2)..... 最后生成的图像如下 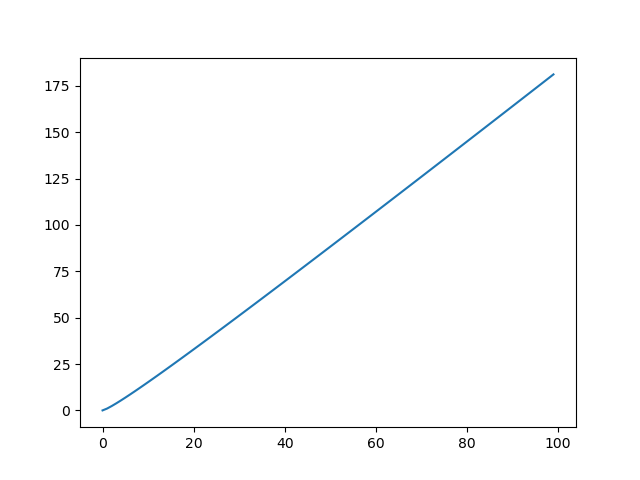 因此,这是个一次函数 然后拟合结果为:```y = 1.856 x - 3.798``` 虽然我觉得这个答案可能不大准确,但是应该算出来的答案误差也不是很大,拿来当估值也是可以的。XD |
12
ITJoker 2020-08-14 23:47:59 +08:00
```y = 1.85631216*x -3.79846311```
|
13
ITJoker 2020-08-15 00:07:37 +08:00
之前的有点问题,用哪个老兄计算的方法,最多可以计算到 109
我重新拟合了下:y = (1.86313312*x -4.0335139) 误差范围: (1.2019039967254912,1.2535931255835067) |
14
ITJoker 2020-08-15 00:17:09 +08:00
正确误差范围:(-0.8856246689377087,4.0335139)
太乌龙了,代码写错了||| |
15
mathzhaoliang OP @ITJoker 这是一份我写的代码,使用了一个递推关系:
令 v_k = f(k, k), p_k = \binom{2k}{k} / 2^{2k},则 v_{k+1} = (1- p_k) / (1 + p_k) v_k + (2k+1) * (2p_k) / (1+P_k) ```python from decimal import * pi = 3.14159265358979 getcontext().prec = 20 def solve_sheep(n): p = [0 for _ in range(n + 1)] v = [0 for _ in range(n + 1)] v[1] = 1 p[1] = Decimal(0.5) for k in range(2, n + 1): p[k] = (1 - 1 / Decimal(2 * k)) * p[k - 1] for k in range(1, n): w = (1 - p[k]) / (1 + p[k]) v[k + 1] = w * v[k] + (1 - w) * (2 * k + 1) return v[n] def estimate_sheep(n): return 2 * n + pi / 4 - (pi * n)**0.5 print(solve_sheep(10000)) print(estimate_sheep(10000)) ``` |
16
spcharc 2020-08-16 17:55:20 +08:00
得到了 f(10000,10000)精确值,存入文件一看有 60M 大,也是无语。试着让 Python 读出来再 eval(),结果一个小时过去都没 load 完…
|
18
jingslunt 2020-08-17 08:56:22 +08:00 via Android
我也出道估计你解不出来的题
odd(n) : while(n>1) if(odd(n)) n=3*n+1; else n=n/2; 其中 odd(n)为奇数。 找出这个递归函数最终值不为 1 的那个 n 值。 |
19
jingslunt 2020-08-17 09:02:46 +08:00 via Android
其中 odd(n)为奇数就执行 if 下的赋值,偶数执行 else 下的赋值,找出最终递归值不唯一的那个 n
|
20
mathzhaoliang OP @spcharc 你运行的代码肯定做了修改,只计算 f(10000, 10000) 的值一秒都用不了。
|
21
mathzhaoliang OP @jingslunt 我出的问题是有确定可行的解的。
|
22
dongyx 2020-08-17 17:16:06 +08:00
有意思的问题。
我目前的思路是动态规划,计算顺序是一条对角线一条对角线地算,不断地填充左上三角。 算第 n 条对角线的时候,其实算一个一维的二阶递推式,需要 O(n)的时间,那么要算 f(n, n)需要 O(n^2),感觉算 f(10000, 100000)有点吃力。我想看看能不能优化一下算一条对角线的做法,可惜系数不是常数,不然就可以矩阵快速幂了。 愿闻楼主高见。 |
23
mathzhaoliang OP @dongyx 如果问题只要求算 f(n, n) 的值,那么所有的 v_n=f(n,n) 之间满足一个递推关系,所以可以快速求解。
如果是计算任意 f(x, y) 的值,那确实就得逐个对角线求解了。这个推导过程可以见我的一篇文章 http://pywonderland.com/mabinogion-sheep-problem/ |
24
ITJoker 2020-08-18 00:16:54 +08:00
|
25
ITJoker 2020-08-18 00:33:09 +08:00
之前思路大概和你差不多,只不过列出来的公式不是这样,确切的是用我推导的那个公式答案算出来有点偏差,所以放弃了那个思路转拟合思路了,数学用的太少了,害😂
|
26
hardwork 2020-08-19 21:31:32 +08:00
每一层都是个方程组,10000 层是 9999 元一次方程组,每个方程组的参数需要上一个方程组的解
计算机递推只想到这种解法。 或者数学上能直接递推出公式? |
27
mathzhaoliang OP @hardwork 对,数学上可以找出递推公式。见 23 楼的链接。
|