这是一个创建于 1487 天前的主题,其中的信息可能已经有所发展或是发生改变。
1
chizuo 2020-11-22 22:27:06 +08:00
这俩一个东西啊。只不过谢希仁语义简写了,不过你通过后面那句“B 对篡改过的报名进行解密”,也能明白啊。
省略了“拿 A 的公钥去解 Dsa ( X ),得到后和 message 比较即可”。而且人家图 7-4 也说得明明白白的 |
2
az467 2020-11-22 22:30:57 +08:00
都一样啊。
第一个直接加密了原文。 第二个加密的是原文的哈希值,原文是公开的。 反正都能确定消息是 A 发的。 除非 A 神经错乱,不然不会给 B 发送乱七八糟的内容,所以就能确定喽。 |
3
huangya OP |
4
Jirajine 2020-11-22 22:40:31 +08:00 via Android
我的理解也是第二个正确。
第一个里面看起来非常不严谨,“得到不可读的明文”这个要如何判断呢? |
5
YetToCome 2020-11-22 22:52:04 +08:00 via Android
乱码只是不可读微小的一部分
|
6
noe132 2020-11-22 23:10:24 +08:00 密文 = 加密(原文, 私钥)
原文 = 解密(密文, 公钥) 并且从数学上,知道 原文、密文、私钥、公钥 中的任意 3 个都无法轻易推算出剩下的一个。 A 只需要保管好 私钥,别人就无法伪造加密过程。 B 只要保证自己的公钥是正确的,那么就能够验证密文是不是由 A 发送过来的。 假设 A 发过来的信息被篡改了,然后被 B 用公钥解密,得到的就肯定不是 A 本来要发的原文。但 B 并不知道这到底就是原文,还是乱码?如何得知解密得到的乱码是不是就是 A 本意要发过来的内容,还是被篡改后的?答案就是用加密做签名,把原文和签名一并发送。 假设 A 想发的信息是 m,对 m 用私钥加密后得到 e,并且对 m 做 hash,得到 hash 值 h,此时将 e(m) 和 h 一并发给 B 。 B 拿到 e 后用公钥解密出原文 m',并且也对 m' 做 hash,得到结果 h'。此时对比 h 和 h' 如果是同一个值,那么 B 认为传输没有被篡改。 如果出现了传输错误或者被篡改,那么 B 得到的 h' 肯定不等于 h,这时 B 就能发现错误。 软件数字签名的原理简单来说就是上面的过程,软件发布者给软件计算 hash,并且用私钥签名,和软件一起发布。用户下载软件后后用公钥解密签名得到 hash,然后和自己计算的 hash' 做对比,如果不一致那么就说明软件被篡改了。 当然前提是用户拿到的是正确的公钥。现在系统都由内置根证书,作为信任保障,然后由根证书签发出新的子证书,用来做加密。因为子证书是根证书签发(和上面加密的过程类似)出来的,没有(根证书)私钥的人没法随便签发证书。只要根证书是有效的,并且大家都认可这个根证书,那么就能保证子证书是正确有效的。 |
7
noe132 2020-11-22 23:21:38 +08:00
为什么 B 通过"不可读的明文"(乱码?)就认为这个不是 A 发的,这样是不是不严谨?
确实不严谨,因为 乱码也是数据。但 谢希仁 只介绍了加密解密的过程,没有介绍防篡改的过程。因为通常来说被窜给的密文解密出有意义的数据概率比较低,应该就用这个简单代替了,但非对称加密的核心是一致的。而且通常来说,防篡改不仅仅是计算一个 hash 这么简单,像计算机网络中还会遇到防重放攻击相关的内容,但核心思路就是用 hash 或者校验和等手段检验数据是否发生了变化。 |
9
catror 2020-11-22 23:27:25 +08:00 via Android
比 hash 是正确的
|
10
geelaw 2020-11-23 01:55:00 +08:00 via iPhone
两本书都有用语上的混乱,前者还有对签名理解上的混乱、对安全性解读的混乱,但经过修补之后都是正确的——即 hash 函数不是签名必备的一部分。
前者对签名理解上的混乱在于赘余表达签名不保护消息的隐秘性,其理由错误,并不是因为任何人都可以“重新加密”,而是因为消息本身总是伴随着签名发送,因而一开始就没有隐秘性。 前者对安全性解读的混乱在于它的表述让人误以为安全 = 无法恢复密钥,这是错误的,签名的安全性是不可伪造,不能还原密钥只是它的一个推论。 两者在用语上的错误在于把签名说成解密、验证说成加密,实际上无此关系。 Hash 函数并不是签名的必备要素,而且签名算法的实现也不止两者所述的样子。 签名算法的消息空间可以是固定长度的,即使想要得到无限长度的消息空间,也不需要 hash 函数(如 Lamport 签名算法加 GGM )。 当然,后者的情况更接近真实世界里的签名算法,也就是使用 hash 函数。 |
11
yeqizhang 2020-11-23 08:09:29 +08:00 via Android
两个都类似,描述不太一样吧,都没啥问题吧。
解密后得出不可读明文,这个不可读,可以说是明文不一致,或者明文不对,hash 也可以说是明文。 最近在研究 https,第二个更像是 https 的证书签名的做法,那个消息就是指服务器公钥和服务器的一些信息 |
12
AkashicRecords 2020-11-23 10:40:54 +08:00
第一个的描述不可读,这个有些模糊,但不是说这就有很大问题了,《密码编码学与网络安全--原理与实践》第七版的的 公钥密码学和 RSA 部分举例公钥密码可以用于认证的图 9.3 就是和谢希仁版的描述大体一样
图片地址( b64 ):aHR0cHM6Ly9pbWd1ci5jb20vVVlCVklETQ== |
13
huangya OP @geelaw
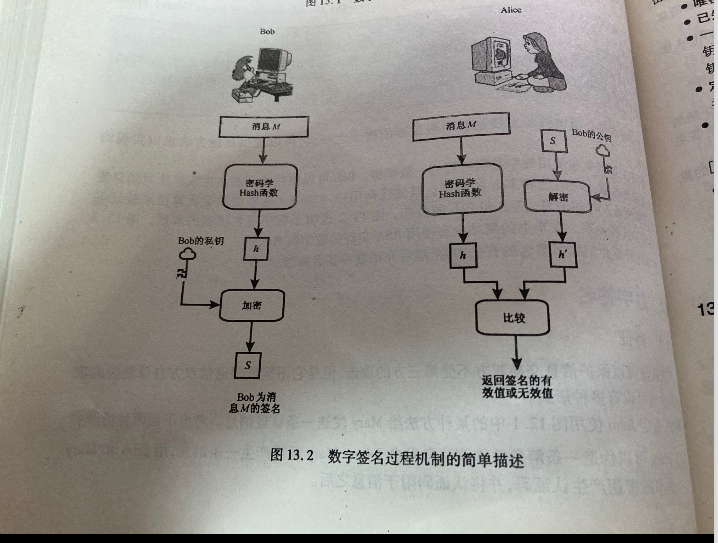
感谢回复. >Hash 函数并不是签名的必备要素,而且签名算法的实现也不止两者所述的样子。 这个其实在后者(《密码编码学与网络安全--原理与实践》)里面有说到,这个图”是产生和使用数字签名的过程的一般模型“,作者没有说 Hash 函数是签名的必备要素,我这是截取了这本书的一个图. |
14
geelaw 2020-11-23 11:49:32 +08:00
@huangya #13 我是根据你的贴图考虑的,不过你援引的这段话里“一般”的理解对正确性有很大影响。如果“一般”理解为“通常”“大多数情况下”(即日常理解),那么是正确的;如果“一般”理解为“恒成立”“总是有”(即数学语言的理解),那么是错误的。
|
15
nnnToTnnn 2020-11-23 15:48:11 +08:00
|
16
nnnToTnnn 2020-11-23 15:52:35 +08:00
D (用来保存公钥信息)
| v ________________________ / \ | | ^ v A (去 D 声明公钥信息) B (去 D 那里获取 A 的公钥) 这样就可以防止被中间人攻击,也就是 https 里面的自签证书,和颁发证书的区别。 |
17
nnnToTnnn 2020-11-23 16:10:20 +08:00
@geelaw 签名和 hash,加密并没有任何关系。
签名,只是为了保证这个“东西” 是由本人编写的。或者本人工作的,因此进行签名。 例如指纹,盖章,亲笔签名,都可以在大多数情况下来证明是由本人签发的,但是实际上,"指纹,盖章,亲笔签名"这些都存在可以伪造签名。 在数字化时代,如何解决签名伪造的问题,成为了一个需求。 在 非对称加密,例如 RSA 或者 ECC 加密算法的出现,才更好的将这种方式实现起来。 public key 可以将 private key 加密的内容给解密出来,在 private key 不泄露的情况下可以保证安全。 例如我可以将这信息进行加密 >>>>>>> rsa( 采用的加密算法 aes , 采用的算法的算法的密钥 123456 ) ======= aes(二进制文件) <<<<<<<< 将这段数据放在服务器上,那么这个签名就成立了。 但是带来第二问题就是,文件太大,没有这么多的空间存放。 于是就有涉及到另外一个算法,散列算法,也就是 hash 算法。例如常见的 sha-256 或者 sha-512 >>>>>>> rsa( 采用的加密算法 aes , 采用的算法的算法的密钥 123456 ) ======= aes(二进制文件 sha 算法) <<<<<<<< 这种签名,可以参照一下 GPG |
18
t9534233 2020-11-27 09:29:49 +08:00 via iPhone
其实说的是一个东西,两者举的例子有点区别,不过第二个看起来确实清晰好理解一点?
因为签名说到底就是要让你知道这个东西确确实实是我发出来的。第一本书举的例子就是根据你看到的解密后内容来判断,比如别人叫你表明身份,你应该回答“我是老王”,你就直接用私钥把“我是老王”加密之后丟出公钥,别人解密一看就能知道。别人想试图冒充你的时候,我拿到密文解密一看,看到的都是乱码,就知道肯定不是你,因为我已经叫你表明身份而不是发乱码。当然你确实是老王但你故意发乱码这个情况不讨论,我肯定也当你不是老王 第二个就是通过 hash 判断,只不过不是直接发出“我是老王”的密文,而是发明文+一个签名而已,至于签名的真伪确认就和上面一样了,我叫你签老王,但签一堆乱七八糟的上去,那你就不是老王 |